Answer:
a) The moment of inertia of the hoop yo-yo rotating about its center of mass is
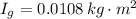 .
.
b) The moment of inertial of the hoop yo-yo rotating about its center of mass is
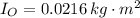 .
.
Step-by-step explanation:
a) The hoop yo-yo can be modelled as a tours with a minor radius
 , related with the thickness, and with a major radius
, related with the thickness, and with a major radius
 , related with the diameter, and with an uniform mass. The momentum of inertia about its center of mass (
, related with the diameter, and with an uniform mass. The momentum of inertia about its center of mass (
 ), measured in kilogram-square meters, which is located at the geometrical center of the element, is determined by the following formula:
), measured in kilogram-square meters, which is located at the geometrical center of the element, is determined by the following formula:
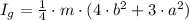 (1)
(1)
 (2)
(2)
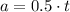 (3)
(3)
Where:
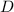 - Diameter, measured in meters.
- Diameter, measured in meters.
 - Thickness, measured in meters.
- Thickness, measured in meters.
 - Mass, measured in kilograms.
- Mass, measured in kilograms.
If we know that
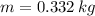 ,
,
 and
and
 , then the moment of inertia of the hoop yo-yo is:
, then the moment of inertia of the hoop yo-yo is:
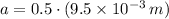
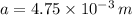

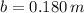
![I_(g) = (1)/(4)\cdot (0.332\,kg)\cdot [4\cdot (0.180\,m)^(2)+3\cdot (4.75* 10^(-3)\,m)^(2)]](https://img.qammunity.org/2021/formulas/physics/college/jjfl4wcs0uu5ikdmmf1js3xlaua44gsq8h.png)
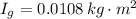
The moment of inertia of the hoop yo-yo rotating about its center of mass is
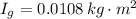 .
.
b) The hoop yo-yo rotate at a point located at a distance of half diameter from the center of mass of the element, whose moment of inertia is determined by the Theorem of Parallel Axes:
 (4)
(4)
Where:
 - Distance between parallel axes, measured in meters.
- Distance between parallel axes, measured in meters.
If we know that
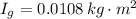 ,
,
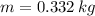 and
and
 , then the moment of inertial of the hoop yo-yo rotating about the point where the tension force is applied is:
, then the moment of inertial of the hoop yo-yo rotating about the point where the tension force is applied is:

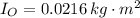
The moment of inertial of the hoop yo-yo rotating about its center of mass is
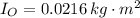 .
.