Answer:
Explanation:
If you plot the vertex and the focus, you'll see that the focus is 2 units above the vertex. That tells us 2 things: first, that the parabola opens upwards and, second, that the value of p in our equation is 2 (since p is the number of units between the vertex and the focus). The equation is:
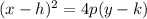 where h and k are the coordinates of the vertex and p is the number of units between the vertex and the focus. The vertex is given as (-6, 8), so h is -6 and k is 8. p is 2, so filling in we get:
where h and k are the coordinates of the vertex and p is the number of units between the vertex and the focus. The vertex is given as (-6, 8), so h is -6 and k is 8. p is 2, so filling in we get:
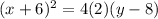 which simplifies down to
which simplifies down to
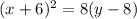
Not sure in what form you need it, so I'll leave it like that and you may have to do some algebraic manipulation to get it into the form your teacher wants it in.