Question

A 2200 kg car moving at 31 m/s comes to a complete stop. What is the work done by the breaks of the car?

Answer 1

The brakes of this car did approximately
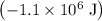`\left(-1.1 * 10^(6)\; \rm J\right)` of work. (Rounded to two significant figures. Assumption: this car is moving horizontally, and that all the lost kinetic energy could be attributed to the braking force.)

Step-by-step explanation:

Is the work of this braking force positive, zero, or negative?

The first step is to find out whether the work of the brakes on the car is greater than zero, smaller than zero, or equal to zero. That could be achieved by comparing:

• the direction of this braking force, and
• the direction in which the target of the braking force (i.e., the rest of the car) has moved.

In this example, the braking force constantly points backwards. On the other hand, the car kept moving forward (until it stopped.)

In other words, the braking force continuously points in the opposite direction of the motion of its target (the car) until the car came to a stop. Therefore, the work of that this braking force has done should be smaller than zero (i.e., negative.)

What is the magnitude of the work that this braking force has done?

Assume that this car is moving horizontally on level ground. Ideally, the amount of work that this braking force has done would be equal to the amount of kinetic energy that this car has lost.

Initial kinetic energy of this car:

`\begin{aligned}& \text{KE(initial)}\\ &= (1)/(2) \, m \cdot {\left(v(\text{initial})\right)}^(2)\\ &= (1)/(2)* 2200\; \rm kg * {\left(31\; \rm m \cdot s^(-1)\right)}^(2) \\ &= 1.0571 * 10^(6)\; \rm J\end{aligned}`.

Kinetic energy of this car after it came to a complete stop:

`\begin{aligned}\text{KE(final)}= 0\; \rm J\end{aligned}`.

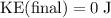Kinetic energy that this car has lost:
`1.0571* 10^(6)\; \rm J`.

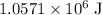That should be the same as the magnitude of the work that this braking force has done. However, because this work is smaller than zero, the actual value of this work would be
`\left(-1.0571* 10^(6)\; \rm J\right)`.

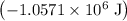In this question, both the mass and the initial speed of this car are specified with only two significant figures each. Hence, round the result accordingly and keep only two significant figures:
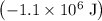`\left(-1.1* 10^(6)\; \rm J\right)`.