Question

In a certain Algebra 2 class of 29 students, 7 of them play basketball and 14 of them

play baseball. There are 10 students who play neither sport. What is the probability
that a student chosen randomly from the class plays basketball or baseball?

Answer 1

Two possible answers below

Explanation:

Probability and Sets

We are given two sets: Students that play basketball and students that play baseball.

It's given there are 29 students in certain Algebra 2 class, 10 of which don't play any of the mentioned sports.

This leaves only 29-10=19 players of either baseball, basketball, or both sports. If one student is randomly selected, then the propability that they play basketball or baseball is:

`\displaystyle P=(19)/(29)`

P = 0.66

Note: if we are to calculate the probability to choose one student who plays only one of the sports, then we proceed as follows:

We also know 7 students play basketball and 14 play baseball. Since 14+7 =21, the difference of 21-19=2 students corresponds to those who play both sports.

Thus, there 19-2=17 students who play only one of the sports. The probability is:

`\displaystyle P=(17)/(29)`

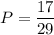
P = 0.59