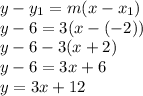Question

I HAVE LESS THEN 10 MINUTES

it’s for geometry
please help:(

Answer 1

Answer:same brooo and nobody is helping me :’(Step-by-step explanation:

Answer 2

y = 3x + 12

Explanation:

For the equation of the perpendicular bisector we have to first find the midpoint of the two end points.

`M(x,y)=((4+(-8))/(2),(4+8)/(2))\\\\M(x,y)=(-2,6)`

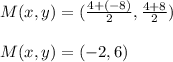
Now we need to find the slope of the line .

`m=(y_2-y_1)/(x_2-x_1)\\\\m= (8-4)/(-8-4)\\\\m=(4)/(-12) \\\\m=-1/3`

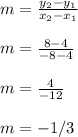
Now the slope of the perpendicular line is,

`m_1m_2=-1\\\\-(1)/(3)m_2=-1\\\\m_2=3`

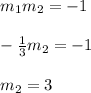
Now to find the equation of line , we use Point-slope form:

`y-y_1=m(x-x_1)\\y-6=3(x-(-2))\\y-6-3(x+2)\\y-6=3x+6\\y=3x+12`