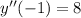Question

Implicit differentiation Please help

Answer 1

Hope this helps you with implicit differentiations

Answer 2

`y''(-1) =8`

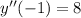
General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Equality Properties

Algebra I

• Factoring

Calculus

Implicit Differentiation

The derivative of a constant is equal to 0

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Product Rule:
`(d)/(dx) [f(x)g(x)]=f'(x)g(x) + g'(x)f(x)`

Chain Rule:
`(d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Quotient Rule:
`(d)/(dx) [(f(x))/(g(x)) ]=(g(x)f'(x)-g'(x)f(x))/(g^2(x))`

Explanation:

Step 1: Define

-xy - 2y = -4

Rate of change of the tangent line at point (-1, 4)

Step 2: Differentiate Pt. 1

Find 1st Derivative

1. Implicit Differentiation [Product Rule/Basic Power Rule]:
   `-y - xy' - 2y' = 0`
2. [Algebra] Isolate y' terms:
   `-xy' - 2y' = y`
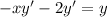
3. [Algebra] Factor y':
   `y'(-x - 2) = y`
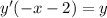
4. [Algebra] Isolate y':
   `y' = (y)/(-x-2)`
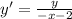
5. [Algebra] Rewrite:
   `y' = (-y)/(x+2)`

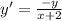
Step 3: Find y

1. Define equation:
   `-xy - 2y = -4`
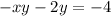
2. Factor y:
   `y(-x - 2) = -4`
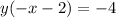
3. Isolate y:
   `y = (-4)/(-x-2)`
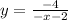
4. Simplify:
   `y = (4)/(x+2)`

Step 4: Rewrite 1st Derivative

1. [Algebra] Substitute in y:
   `y' = (-(4)/(x+2) )/(x+2)`
2. [Algebra] Simplify:
   `y' = (-4)/((x+2)^2)`

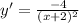
Step 5: Differentiate Pt. 2

Find 2nd Derivative

1. Differentiate [Quotient Rule/Basic Power Rule]:
   `y'' = (0(x+2)^2 - 8 \cdot 2(x + 2) \cdot 1)/([(x + 2)^2]^2)`
2. [Derivative] Simplify:
   `y'' = (8)/((x+2)^3)`

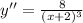
Step 6: Find Slope at Given Point

1. [Algebra] Substitute in x:
   `y''(-1) = (8)/((-1+2)^3)`
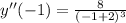
2. [Algebra] Evaluate:
   `y''(-1) =8`