Question

Exit

5-3: MathXL for School: Practice & Problem Solving
Du
5.3.PS-12
Question Help
A family buys 5 airline tickets online. The family buys travel insurance that costs $19 per ticket.
The total cost is $850. Let x represent the price of one ticket. Write an equation for the total Cost
Then find the price of one ticket.
Which equation represents this situation?
O A. 850 = 5x + 19
OB. 850 = 19(x + 5)
OC. 19 = 5x + 850
D. 850 = 5(x +19)
The price of one ticket is $.
Enter your answer in the answer box and then click Check Answer
Clear All
All parts showing
Chikan
Review progress
Back
Next →

Answer 1

The equation that represents the situation is:
`\mathbf{850=5(x+19)}`

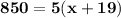
Option D is correct option.

The price of one ticket = $151

Explanation:

Total number of tickets = 5

Cost of insurance per ticket = $19

Total Cost of tickets = $850

Let:

Cost of one ticket = x

Total cost of one ticket will be cost of ticket plus insurance i.e. x+19

Now, family bought 5 tickets so, total cost of 5 tickets will be:

`\mathbf{850=5(x+19)}`

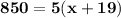
Therefore, the equation that represents the situation is:
`\mathbf{850=5(x+19)}`

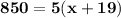
Option D is correct option.

Now, solving the equation to find price of one ticket i.e value of x

`850=5(x+19)\\850=5x+95\\Switching\:sides\\5x+95=850\\5x=850-95\\5x=755\\Divide\:both\:sides\:by\:5\\(5x)/(5)=(755)/(5)\\x=151`

So, we get the value of x = 151

So, The price of one ticket = $151