Question

• Let f be a function such that f(-2) = 8 and f'(-2) = 4.

• Let h be the function h(x) = x3.
Evaluate
d f(x)
dx h(x)
at x = -2.
Show Calculator

Answer 1

-2

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Calculus

Derivatives

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Quotient Rule:
`(d)/(dx) [(f(x))/(g(x)) ]=(g(x)f'(x)-g'(x)f(x))/(g^2(x))`

Explanation:

Step 1: Define

`(d)/(dx) [(f(x))/(h(x)) ] \ at \ x = -2\\h(x) = x^3\\f(-2) = 8\\f'(-2) = 4`

Step 2: Differentiate

1. Differentiate [Quotient Rule]:
   `(d)/(dx) [(f(x))/(h(x)) ] = (f'(x)h(x) - f(x)h'(x))/(h(x)^2)`
2. Differentiate h(x) [Basic Power]: h'(x) = 3x²

Step 3: Evaluate

1. Define differential:
   `(f'(x)x^3 + f(x)[3x^2])/((x^3)^2)`
2. Substitute in variables:
   `(f'(-2)h(-2) + f(-2)h'(-2))/(h(-2)^2)`
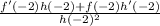
3. Substitute in variables:
   `(4(-2)^3 - 8[3(-2)^2])/([(-2)^3]^2)`
4. Evaluate: -2