Answer:
Radius = 4 cm
Area = 16π cm²
Volume = 240π cm³
Explanation:
Radius of the given cylinder =
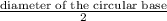
=
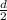
=
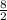
= 4 cm
Area of the circular base =
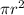
Here 'r' = radius of the circular base
Area of the base =
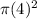
= 16π cm²
Volume of a cylinder is given by the formula,
V = πr²h
Here 'r' = radius of the circular base
h = height of the cylinder
By substituting the values in the formula,
V = π(4)²(15)
= 240π cm³