Question

A survey asked 26 adults how many years of education they had. The sample mean was 13.03 with a standard deviation of 3.22. It is reasonable to assume that the population is approximately normal. Construct a 90% confidence interval for the mean number of years of education. (I saw this one on g when I tried to socratic it.

Answer 1

Answer: (11.95, 14.11)

Step-by-step explanation:

Let x be a random variable that represent the number of years of education.

Given: Sample size : n= 26

Sample mean :
`\overline{x}=13.03`

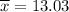
Sample standard deviation : s = 3.22

Significance level :
`\alpha=100\%-90\%=10\%=0.1`

Degree of freedom: df = n-1 = 25

Critical t-value for
`\alpha=0.1` and df = 25 will be

`t_(\alpha/2, df)=t_(0.05,25)=1.7081`

90% confidence interval for mean:

`\overline{x}\pm t_(\alpha/2,df)(s)/(√(n))\\\\=13.03\pm (1.7081)(3.22)/(√(26))\\\\=13.03\pm (1.7081)(3.22)/(5.09902)\\\\=13.03\pm 1.08\\\\=(13.03-1.08,\ 13.03+1.08)\\\\ =(11.95,\ 14.11)`

A 90% confidence interval for the mean number of years of education = (11.95, 14.11)