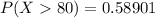Question

The test results for a class with 24 students are normally distributed with a mean of 82 and a standard deviation of 8.9. What is the probability that a randomly chosen student earned a B or higher on the test (score of 80 or higher)?

Answer 1

The value is
`P( X > 80 ) = 0.58901`

Explanation:

From the question we are told that

The sample size is n = 24

The mean is
`\mu = 82`

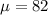
The standard deviation is
`\sigma = 8.9`

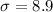
Generally the probability that a randomly chosen student earned a B or higher on the test (score of 80 or higher ) is mathematically represented as

`P( X > 80 ) = P( ( X - \mu )/(\sigma ) > ( 80 - 82 )/( 8.9 ) )`

`(X -\mu)/(\sigma )  =  Z (The  \ standardized \  value\  of  \ X )`

=>
`P( X > 80 ) = P(Z > -0.225 )`

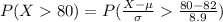
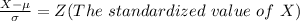
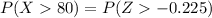
From the z table the area under the normal curve to the right corresponding to -0.225 is

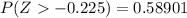
`P(Z > -0.225 ) = 0.58901`

=>
`P( X > 80 ) = 0.58901`