Answer:
Answer B (Increased by 2%)
Step-by-step explanation:
Recall that the period (T) of a pendulum doesn't depend on the pendulum's mass, but depends on the pendulum's length (L) and on the local acceleration of gravity (g) via the formula:

There fore, if the length of the pendulum is increased by 4% (0.04 in decimal form), then the new length becomes: L + 0.04 L = 1.04 L
and therefore the period will change by:
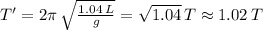
Which means that the period was increased to about 2 % :
T + 0.02 T = 1.02 T