Question

. Find the general solution to

d²y/dx²= 49y. Enter your answer as an equation y = ..

Note: d²y/dx²=k^2y

Answer 1

The given differential equation is linear with constant coefficients,

`(d^2y)/(dx^2) - 49y = 0`

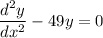
with characteristic equation

`r^2 - 49 = 0`

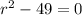
and hence characteristic roots
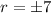`r=\pm7`. This means the general solution to the ODE is

`y = C_1 e^(7x) + C_2 e^(-7x)`

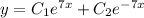
In fact, you're given the solution already,

`y = C_1 e^(kx) + C_2 e^(-kx)`

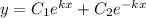
and you've determined that

`(d^2y)/(dx^2) = k^2 (C_1 e^(kx) + C_2 e^(-kx)) = k^2 y`

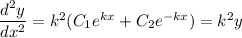
Comparing this to the given ODE, it's obvious that
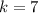`k=7`, so you can just replace
`k` with 7 in the given template solution.