Question

A consultant advises the owners of a phone company that their profit

p each month car-be modeled by
p(x) = -50x2 + 3500x - 2500
The variable x is the average cost that a customer is charged. What
range of costs will bring in a profit of at least $40,000?

Answer 1

$15.63 ≤ x ≤ $54.365

Explanation:

Profit of the phone company is modeled by the equation,

p(x) = -50x² + 3500x - 2500

For the profit of at least $40000,

-50x² + 3500x - 2500 ≥ 40000

-50x² + 3500x ≥ 40000 + 2500

-50x² + 3500x ≥ 42500

-x² + 70x ≥ 850

x² - 70x + 850 ≤ 0

By quadratic formula,

x - intercept of the inequality will be,

x =
`(-(-70)\pm √((-70)^2-4(1)(850)))/(2(1))`

x =
`(70\pm √(1500))/(2)`

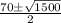
x = 15.635, 54.365

Therefore, $15.635 ≤ x ≤ $54.365 will be the range of cost for which profit will be at least $40000.