Question

1. What is the fundamental frequency (in Hz) of a 72.4 cm long tube, open at both ends, on a day when the speed of sound is 344 m/s?2. What is the frequency of its second hormonic?

Answer 1

The frequency of its second harmonic is 475.14 Hz.

Step-by-step explanation:

Given;

length of the open tube, L = 72.4 cm = 0.724 m

speed of sound, v = 344 m/s

the wavelength at fundamental frequency is calculated as;

L = A -----N + N----A

where;

L is length of the tube

A is antinode of wave in the pipe

N is node of the wave in the pipe

`L = (\lambda)/(4) + (\lambda)/(4)\\\\L = (\lambda)/(2)\\\\\lambda = 2L = \lambda_o`

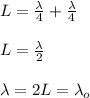
the fundamental frequency of the wave is calculated as;

`f = (v)/(\lambda)\\\\f_o =(v)/(\lambda _o) \\\\f_o = (v)/(2L) \\\\f_o = (344)/(2* 0.724)\\\\f_o = 237.57 \ Hz`

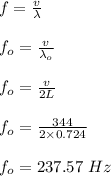
the frequency of the second harmonic is calculated as;

2f₀ = 2 x 237.57

2f₀ = 475.14 Hz.