A company makes electric motors. The probability an electric motor is defective is 4%. What is the probability that a sample of 60 electric motors will contain exactly 2 defecti…

Question

asked Dec 28, 2021 199k views

1 Answer

Braydon Batungbacal · Answer 1 · 2022-01-01T14:32:08+0000

Answer:

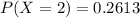
P(X = 2) = 0.2613

Explanation:

Given

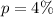$p = 4\%$ --- proportion

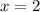x = 2 --- defective motors

n = 60 --- sample size

Required

Determine the probability that exactly 2 is defective

This follows a Poisson distribution and will be solved using:

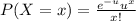
P(X = x) = (e^(-u) u^x)/(x!)

Where

u = Expected number of occurrence, and it is calculated as:

u = np

$u = 60 * 4\%$

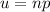
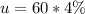
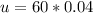
u = 60 * 0.04

u = 2.4

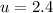
So:

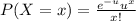P(X = x) = (e^(-u) u^x)/(x!) becomes

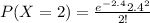
P(X = 2) = (e^(-2.4)2.4^(2))/(2!)

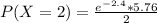
P(X = 2) = (e^(-2.4)* 5.76)/(2)

P(X = 2) = e^(-2.4)* 2.88

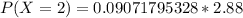
P(X = 2) = 0.09071795328* 2.88

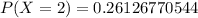
P(X = 2) = 0.26126770544

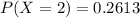
P(X = 2) = 0.2613

Hence, the probability that exactly 2 out of 60 will be defective is 0.2613