Question

Use the inermediate value Theorem to choose an interval over which the function f(x)=-2x^3-3x+5, is guaranteed to have a zero.

1. [-3,-2]
2. [-2,0]
3. [0,2]
4. [2,4]

Answer 1

Choice 3: [0, 2]

Explanation:

The Intermediate Value Theorem states that if we have a continuous function f over the interval [a, b] and k is a number between f(a) and f(b), then there must at least one point c within [a, b] such that f(c)=k.

Then, by the IVT, if the endpoints differ in signs, then we must have a zero within the interval since f must cross the x-axis in order to change signs.

So, we will test the endpoint values for each interval.

We have the function:

`f(x)=-2x^3-2x+5`

Choice 1:

Testing for the endpoints, we get:

`\begin{aligned} f(-3)&=-2(-3)^3-3(-3)+5\\&=68\end{aligned}`

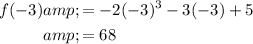
And:

`\begin{aligned} f(-2)&=-2(-2)^3-3(-2)+5\\&=27\end{aligned}`

Since both values are positive, we are not guaranteed a zero for the interval [-3, -2].

Choice 2:

Testing endpoints, we get:

`f(-2)=27\text{ and } f(0)=5`

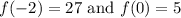
Again, both values are positive, so we are not guaranteed a zero.

Choice 3:

We get:

`f(0)=5\text{ and } f(2)=-17`

Since the values are of different signs, by the IVT, we are guaranteed a zero by for the interval [0, 2] since the function must cross the x-axis in order to become negative.

So, Choice 3 is correct.

Choice 4:

We get:

`f(2)=-17\text{ and } f(4)=-135`

Both values are negative, so we are not guaranteed a zero.

Note: We may have a zero for the other three intervals. For instance, for [-3, -2], maybe we went from positive to negative to positive again all within the interval [-3, -2]. However, the only interval that guarantees a zero will be C.