Answer:
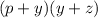
=======================================
Work Shown:
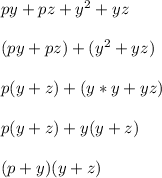
I grouped the terms into pairs. Then I factored the GCF from each pair
The GCF of py+pz is p
The GCF of y^2+yz is y
On the last line, I factored out the overall GCF (y+z)
You can use the FOIL rule or the distributive property to expand out (p+y)(y+z) and you should get the original expression back again. This is a way to confirm the correct answer.