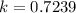Question

Unpolarized light passes through two polarizers whose transmission axes are at an angle of 42.0 degrees with respect to each other. What fraction of the incident intensity is BLOCKED by the polarizers

Answer 1

The value is
`k = 0.7239`

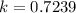
Step-by-step explanation:

From the question we are told that

The angle between the transmission axes of the polarizer
`\theta = 42^o`

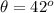
Gnerally the intensity light emerging from the first polarizer is

`I_1 = (I_o )/(2)`

Generally according to malus's law the intensity of light emerging from the second polarizer is mathematically represented as

`I_2 = I_1 * cos^(2) (\theta )`

=>
`I_2 = (I_o )/( 2) * cos^(2) (42 )`

=>
`I_2 = 0.2761 I_o`

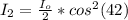
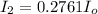
Generally the incident intensity is BLOCKED by the polarizers is mathematically represented as

`I = I_o - I_2`

=>
`I = I_o - 0.2761 I_o`

=>
`I = 0.7239 \ I_o`

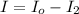
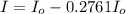
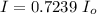
Hence the fraction of the incident intensity is BLOCKED by the polarizers is

`k = 0.7239`