Question

A car starts from rest at the top of a hill with 45 J of gravitational

potential energy. If it has a mass of 3 kg, how fast will it be moving
at the bottom of the hill?

Answer 1

The car will be moving at 5.48 m/s at the bottom of the hill

Step-by-step explanation:

Principle of Conservation of Mechanical Energy

In the absence of friction, the total mechanical energy is conserved. That means that

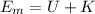`E_m=U+K` is constant, being U the potential energy and K the kinetic energy

U=mgh

`\displaystyle K=(mv^2)/(2)`

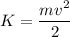
When the car is at the top of the hill, its speed is 0, but its height h should be enough to produce the needed speed v down the hill.

The Kinetic energy is then, zero. When the car gets enough speed we assume it is achieved at ground level, so the potential energy runs out to zero but the Kinetic is at max. So the initial potential energy is transformed into kinetic energy.

We are given the initial potential energy U=45 J. It all is transformed to kinetic energy at the bottom of the hill, thus:

`\displaystyle (mv^2)/(2)=45`

Multiplying by 2:

`\displaystyle mv^2=90`

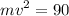
Dividing by m:

`\displaystyle v^2=(90)/(m)`

Taking square roots:

`\displaystyle v=\sqrt{(90)/(m)}`

`\displaystyle v=\sqrt{(90)/(3)}`

`v=√(30)`

v = 5.48 m/s

The car will be moving at 5.48 m/s at the bottom of the hill