Question

The average mass for a spacesuit plus astronaut is 191 kg. The average speed for air molecules inside the space suit is 549 m/s and has a density of 1.05 kg/m^3. If the air escapes Whatney's suit at 0.020 m^3/s moving directly away from him, how fast will he be going after 8.1 seconds (in m/s) if he started from rest?

Answer 1

The value is
`v_a = 0.489 \ m/s`

Step-by-step explanation:

From the question we are told that

The mass of the spacesuit plus astronaut is
`m = 191 \ kg`

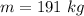
The average speed of air molecules is
`v = 549 \ m/s`

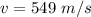
The density of air molecule is
`\rho = 1.05 \ kg / m^3`

The acceleration of the air from Whatney's suit is
`a = 0.020 \ m/s^2`

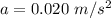
The time considered is
`t = 8.1 \ s`

Generally the mass of air that have left Whatney's suit after the time considered is mathematically represented as

`M = a * \rho * t`

=>
`M = 0020 * 1.05 * 8.1`

=>
`M = 0.1701 \ kg`

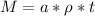
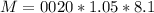
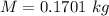
Generally the momentum of the escaped air is

`p = M * v`

=>
`p = 0.1710 * 549`

=>
`p = 93.38 \ kg \cdot m/s`

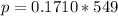
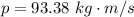
Generally from the law of momentum conservation

`p = p_a`

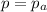
Here
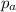`p_a` is the momentum of the astronaut at the considered time

`93.38 = m * v_a`

Here
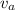`v_a` is the velocity of the astronaut at the considered time

=>
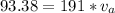
`93.38 = 191 * v_a`

=>
`v_a = 0.489 \ m/s`