Question

(x^3-2x^2-75) divided by (x-5)

Answer 1

Hello!

`\large\boxed{x^(2) + 3x + 15}`

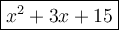
To solve, we can use polynomial long division:

Set up the process using (x³ - 2x² - 75) as the dividend. Put in a place holder of (0x) to ensure that a proper answer is reached.

Use (x - 5) as the divisor.

Steps for dividing:

1. Find how many times that the first term in the divisor will go into the first term of the dividend. In the first step, (x - 5) goes into (x³ - 2x²) x² times. Put this at the top for our quotient .

2. Multiply both of the terms in the divisor by x². Put those expressions underneath the dividend and subtract.

3. Bring down the next number in the dividend and find how many times (x - 5) goes into 3x² + 0x. We get 3x times, so repeat the same steps above.

4. Continue until you finish with the last two numbers. If the remainder is 0, your solution is simply the quotient at the top. (In this instance).