Hi there! :)
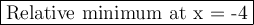
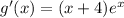
Find the critical point by setting g'(x) to 0:
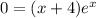
Set each factor equal to 0:
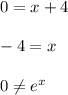
Therefore, the only critical point is at x = -4. Test to see whether this is a relative min or max by plugging in values on both sides into the equation for g'(x):

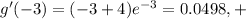
The graph changes from - to + at x = -4, so there is a relative minimum at x = -4.