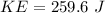Question

A merry-go-round on a playground consists of a horizontal solid disk with a weight of 805 N and a radius of 1.58 m. A child applies a force 49.5 N tangentially to the edge of the disk to start it from rest. What is the kinetic energy of the merry-go-round disk (in J) after 2.95 s?

Answer 1

The value is
`KE = 259.6 \ J`

Step-by-step explanation:

From the question we are told that

The weight of the horizontal solid disk is
`W = 805 \ N`

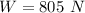
The radius of the horizontal solid disk is
`r = 1.58 \ m`

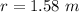
The force applied by the child is
`F = 49.5 \ N`

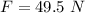
The time considered is
`t = 2.95 \ s`

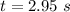
Generally the mass of the horizontal solid disk is mathematically represented as

`m_h = (W)/( g)`

=>
`m_h = (805)/( 9.8 )`

=>
`m_h = 82.14 \ N`

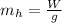
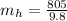
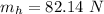
Generally the moment of inertia of the horizontal solid disk is mathematically represented as

`I = (1)/(2) * m * r^ 2`

=>
`I = (1)/(2) * 82.14 * 1.58^ 2`

=>
`I = 102.5 \ kg \cdot m^2`

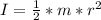
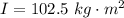
Generally the net torque experienced by the horizontal solid disk is mathematically represented as

`T = I * \alpha = F * r`

=>
`\alpha = ( F * r )/( I )`

=>
`\alpha = ( 49.5 * 1.58 )/( 102.53 )`

=>
`\alpha = 0.7628`

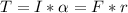
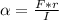
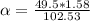
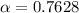
Gnerally from kinematic equation we have that

`w = w_o + \alpha t`

Here
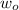`w_o` is the initial angular velocity velocity of the horizontal solid disk which is
`w_o = 0\ rad/s`

So

`w = 0 + 0.7628 * 2.95`

=>
`w = 2.2503 \ rad/s`

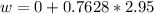
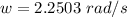
Generally the kinetic energy is mathematically represented as

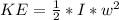
`KE = (1)/(2) * I * w^2`

=>
`KE = (1)/(2) * 102.53 * 2.2503 ^2`

=>
`KE = 259.6 \ J`