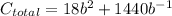Answer:
Base=3.42cm
Height = 10.26 cm
For a total cost of $631.59
Explanation:
In order to solve this problem we can start by drawing what the box will look like. (See attached picture).
So, the problem mentions that the box will have a volume of
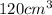 . Since the box has a squared base, we can calculate its volume by using the following formula:
. Since the box has a squared base, we can calculate its volume by using the following formula:

we can turn this into an equation by substituting the corresponding volume:
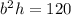
now, the problem tells us that the base of the box will cost
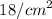 so first, we need to calculate the area of the base of the box. Its area can be calculated by using the following formula:
so first, we need to calculate the area of the base of the box. Its area can be calculated by using the following formula:
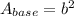
so the cost of the base is calculated with the following equation:
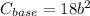
we can find the cost of the sides of the box by following a similar procedure:
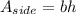
since there are 4 sides to the box, then we can calculate the total area of the sides by multiplying the formula by 4.
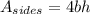
the problem tells us that the cost of the sides of the container is:
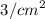 so the cost of the sides will be:
so the cost of the sides will be:
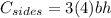
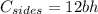
So the total cost of the box is found by adding the two costs we just found:
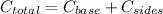

so we can take the volume equation to find an equation we can substitute for h on the cost equation:

when substituting we get:
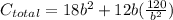
Which simplifies to:
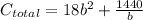
or:
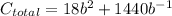
In order to minimize the costs we will now take the derivaative of this function and set it to be equal to zero:
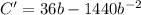
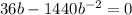
and now we solve for b:
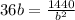
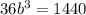
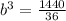
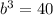
![b=\sqrt[3]{40}](https://img.qammunity.org/2021/formulas/mathematics/college/xdazzojw2tq8opgxj1idj77c5ft5yzmf3r.png)
b=3.42 cm
so now we can use this value to find the height:
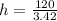
h=10.26 cm
the total cost is found by using the cost equation: