Answer:
The positions are 0.0194 m and - 0.0194 m.
Step-by-step explanation:
Given;
amplitude of the simple harmonic motion, A = 2.0 cm = 0.02 m
speed of simple harmonic motion is given as;
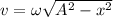
the maximum speed of the simple harmonic motion is given as;
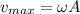
when the speed equal one fourth of its maximum speed
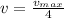
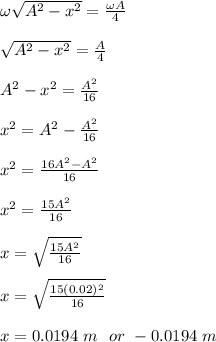
Thus, the positions are 0.0194 m and - 0.0194 m.