Question

An unknown radioactive sample is observed to decrease in activity by a factor of two in a one hour period. What is its half-life?

Answer 1

The half-life is
`t_(1/2) = 1.005 h`

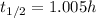
Step-by-step explanation:

Using the decay equation we have:

`A=A_(0)e^(-\lambda t)`

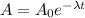
Where:

• λ is the decay constant
• A(0) the initial activity
• A is the activity at time t

We know the activity decrease by a factor of two in a one hour period (t = 1 h), it means that
`A = (A_(0))/(2)`

`(A_(0))/(2)=A_(0)e^(-\lambda*1 h)`

`0.5=e^(-\lambda*1 h)`

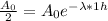
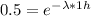
Taking the natural logarithm on each side we have:

`ln(0.5)=-\lambda`

`\lambda=0.69 h^(-1)`

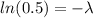
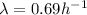
Now, the relationship between the decay constant λ and the half-life t(1/2) is:

`\lambda = (ln(2))/(t_(1/2))`

`t_(1/2) = (ln(2))/(\lambda)`

`t_(1/2) = (ln(2))/(0.69)`

`t_(1/2) = 1.005 h`

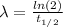
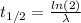
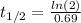
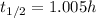
I hope it helps you!