Answer: Final temperature is 34.15°C.
Step-by-step explanation: When two objects have different temperature, they will exchange heat energy until there is no more net energy transfer between them. At that state, the objects are in thermal equilibrium.
So, when in equilibrium, the total heat flow must be zero, i.e.:
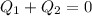
In our case, there will be a change in state of ice into water, so total heat flow will be:
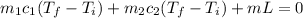
where
m₁ is mass of ice
m₂ is mass of water
c₁ is specific heat of ice
c₂ is specific heat of water
 is final temperature
is final temperature
 is initial temperature
is initial temperature
L is latent heat fusion
Temperature is in Kelvin so the transformation from Celsius to Kelvin:
For ice:
T = -15 + 273 = 258K
For water:
T = 48 + 273 = 321K
Solving:
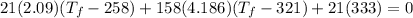
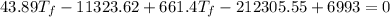
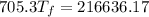
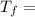 307.15K
307.15K
In Celsius:
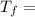 34.15°C
34.15°C
Final temperature of the system when in equilibrium is 34.15°C