Answer:
The apparent depth d = 19.8495 cm
Step-by-step explanation:
The equation for apparent depth can be expressed as:
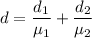
here;
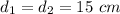
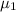 = refractive index in the first liquid = 1.75
= refractive index in the first liquid = 1.75
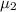 = refractive index in the second liqquid= 1.33
= refractive index in the second liqquid= 1.33
∴
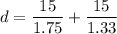
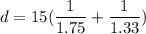
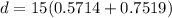
d = 15(1.3233 ) cm
d = 19.8495 cm