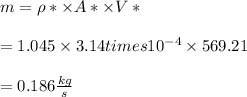Question

Air in a large tank at 300C and 400kPa, flows through a converging diverging nozzle with throat diameter 2cm. It exits smoothly at a Mach number 2.8. According to one-dimensional isentropic theory, what is

(a) exit diameter and
(b) mass flow?

Answer 1

The answer is "
`3.74 \ cm\ \ and \ \ 0.186 (kg)/(s)`"

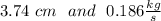Step-by-step explanation:

Given data:

Initial temperature of tank
`T_1 = 300^(\circ)\ C= 573 K`

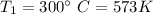
Initial pressure of tank
`P_1= 400 \ kPa`

Diameter of throat
`d* = 2 \ cm`

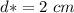
Mach number at exit
`M = 2.8`

In point a:

calculating the throat area:

`A*=(\pi)/(4) * d^2`

`=(\pi)/(4) * 2^2\\\\=(\pi)/(4) * 4\\\\=3.14 \ cm^2`

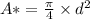
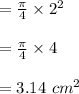
Since, the Mach number at throat is approximately half the Mach number at exit.

Calculate the Mach number at throat.

`M*=(M)/(2)\\\\=(2.8)/(2)\\\\=1.4`

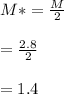
Calculate the exit area using isentropic flow equation.

`(A)/(A*)= ((\gamma -1)/(2))^{(\gamma +1)/(2(\gamma -1))} ((1+(\gamma -1)/(2) M*^2)/(M*))^{(\gamma +1)/(2(\gamma -1))}`

Here:
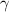`\gamma` is the specific heat ratio. Substitute the values in above equation.

`(A)/(3.14)= ((1.4-1)/(2))^{-(1.4+1)/(2(1.4 -1))} ((1+(1.4-1)/(2) (1.4)^2)/(1.4))^{(1.4+1)/(2(1.4-1))} \\\\A=(\pi)/(4)d^2 \\\\10.99=(\pi)/(4)d^2 \\\\d = 3.74 \ cm`

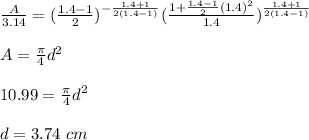
exit diameter is 3.74 cm

In point b:

Calculate the temperature at throat.

`(T*)/(T)=(1+(\Gamma-1)/(2) M*^2)^(-1)\\\\(T*)/(573)=(1+(1.4-1)/(2) (1.4)^2)^(-1)\\\\T*=411.41 \ K`

Calculate the velocity at exit.

`V*=M*√( \gamma R T*)`

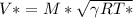
Here: R is the gas constant.

`V*=1.4 * √(1.4 * 287 * 411.41)\\\\=569.21 \ (m)/(s)`

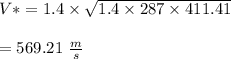
Calculate the density of air at inlet

`\rho_1 =(P_1)/(RT_1)\\\\=(400)/( 0.287 * 573)\\\\=2.43\ (kg)/(m^3)`

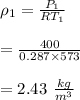
Calculate the density of air at throat using isentropic flow equation.

`(\rho)/(\rho_1)=(1+(\Gamma -1)/(2) M*^2)^{-(1)/(\Gamma -1)} \\\\(\rho *)/(2.43)=(1+(1.4-1)/(2) (1.4)*^2)^{-(1)/(1.4-1)} \\\\\rho*= 1.045 \ (kg)/(m^3)`

Calculate the mass flow rate.

`m= \rho* * A* * V*\\\\= 1.045 * 3.14 times 10^(-4) * 569.21\\\\= 0.186 (kg)/(s)`