Answer:
c. (10.1, 15.7)
Explanation:
The calculation of the 95% confidence interval is shown below:
Given that
n = sample = 14
average =
 = 12.9
= 12.9
Standard deviation = s = 4.9
Based on the above information
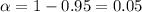
n - 1 = 14 - 1 = 13
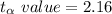
Now the 95% confidence interval is
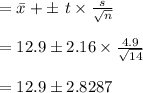
= (10.1, 15.7)
hence, the correct option is c.