Question

The business college computing center wants to determine the proportion of business students who have personal computers (PCʹs) at home. If the proportion exceeds 25%, then the lab will scale back a proposed enlargement of its facilities. Suppose 200 business students were randomly sampled and 65 have PCʹs at home. Find the rejection region for this test using α = 0.01. (Note that this is a right-tailed test).

A) Reject H0 if 0 z > 2.33.
B) Reject H0 if 0 z < -2.33.
C) Reject H0 if 0 z > 2.575 or z < -2.575.
D) Reject H0 if 0 z = 2.
Find the test statistic, 0 t , to test the claim about the population mean μ < 6.7 given n = 20, x = 6.3, s = 2.0.
A) -1.233
B) -0.872
C) -1.265
D) -0.894
Determine the test statistic, 0 z , to test the claim about the population proportion p < 0.85 given n = 60 and x = 39.
A) -4.34
B) -1.96
C) -1.85
D) -1.76

Answer 1

Question 5

correct option is A

Question 6

correct option is D

Question 7

correct option is A

Explanation:

Considering question 5

From the question we are told that

The population proportion considered is
`p = 0.25`

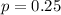
The sample size is n = 200

The number that had a personal computer at home is
`k = 65`

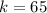
The level of significance is
`\alpha = 0.01`

The null hypothesis is
`H_o : p = 0.25`

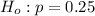
The alternative hypothesis is
`H_a : p > 0.25`

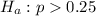
Generally from the z-table the critical value of
`\alpha = 0.01` to the right of the curve is

`z_(\alpha ) = 2.33`

Generally given that it is a right-tailed test , the rejection region is

z > 2.33

Considering question 6

The sample size is n = 20

The standard deviation is
`s = 2`

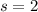
The sample mean is
`\=x = 6.3`

The population mean
`\mu = 6.7`

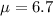
Generally the test statistics is mathematically represented as

`t = ( \= x - \mu )/((s)/(√(n) ) )`

=>
`t = ( 6.3 - 6.7 )/( ( 2)/( √(20) ) )`

=>
`t = -0.894`

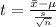
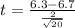
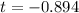
Considering question 7

The sample size is n = 60

The sample mean is
`x = 39`

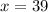
The population proportion
`p = 0.85`

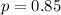
Gnerally the sample proportion is mathematically represented as

`\^ p = (x)/(n)`

=>
`\^ p = (39)/(60)`

=>
`\^ p = 0.65`

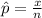
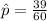
Generally the standard error of this distribution is mathematically represented as

`SE = \sqrt{ ( p(1 - p ) )/( n ) }`

=>
`SE = \sqrt{ ( 0.85 (1 - 0.85 ) )/( 60 ) }`

=>
`SE = 0.0461`

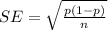
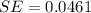
Generally the test statistics is mathematically represented as

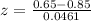
`z = ( \^ p - p )/(SE)`

=>
`z = ( 0.65 - 0.85 )/(0.0461)`

=>
`z = -4.34`