(a) Given
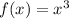 , the derivative is
, the derivative is
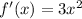
which is exists for all
 in the domain of
in the domain of
 , so
, so
![]f](https://img.qammunity.org/2023/formulas/mathematics/college/3l93aiqqswtjonfpywqx083caorqof1fw1.png) is differentiable everywhere and satisfies the mean value theorem. There is some number
is differentiable everywhere and satisfies the mean value theorem. There is some number
 in the open interval (0, 2) such that
in the open interval (0, 2) such that
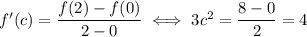
Solve for
 :
:
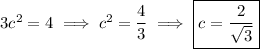
We omit the negative square root since it doesn't belong to (0, 2). Graphically, the MVT tells us the tangent line to the curve
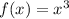 at
at
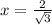 is parallel to the secant line through the endpoints of the given interval.
is parallel to the secant line through the endpoints of the given interval.
(b)
 has derivative
has derivative
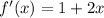
By the MVT,
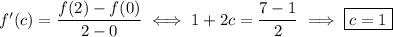
(c)
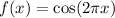 has derivative
has derivative
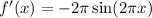
By the MVT,
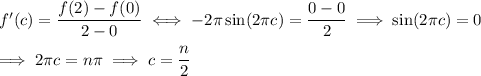
where
 is any integer. There are 3 solutions in the interval (0, 2),
is any integer. There are 3 solutions in the interval (0, 2),

(Pictured is the situation with
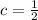 )
)