Answer:
v = 12.4 [m/s]
Step-by-step explanation:
With the speed and Area information, we can determine the volumetric flow.
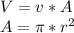
where:
r = radius = 0.0120 [m]
v = 2.88 [m/s]
![A=\pi *(0.0120)^(2) \\A=4.523*10^(-4) [m]\\](https://img.qammunity.org/2021/formulas/physics/college/pmzu1p36m98h13luqjbrrvdix7p5i0e2r6.png)
Therefore the flow is:
![V=2.88*4.523*10^(-4) \\V=1.302*10^(-3) [m^(3)/s ]](https://img.qammunity.org/2021/formulas/physics/college/tn0sfa3exbvhzb8fup4hp68wchf65aqcr9.png)
Despite the fact that you cover the inlet with the finger, the volumetric flow rate is the same.
![v=V/A\\v=1.302*10^(-3) /1.05*10^(-4) \\v=12.4[m/s]](https://img.qammunity.org/2021/formulas/physics/college/hyilrzvyqmaq0j15e5kfj7r0r35vcfl8rp.png)