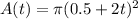Answer:
Explanation:
Given
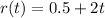
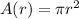
Required
Determine composite function to find A in terms of t
The interpretation of this question is to determine A(t) and this is solved as follows:
Because:
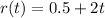
And we want to eliminate r in
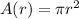
We have to substitute 0.5 + 2t for r in
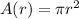
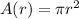 becomes
becomes
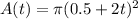
The solution can be solved further, but it is best left in this form: