Question

Given P = x^0.3 y^0.7 is the chicken lay eggs production function, where P is the number of eggs lay, x is the number of workers and y is the daily operating budget.

a) dy/dx
b) Evaluate this derivative at x = 30 and y = 10,000 and interpret the answer.​

Answer 1

Part A)

`\displaystyle (dy)/(dx)=-(3)/(7)P^(10)/(7)x^{-(10)/(7)}`

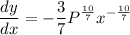
Part B)

The daily operating cost decreases by about $143 per extra worker.

Explanation:

We are given the equation:

`\displaystyle P=x^{(3)/(10)}y^{(7)/(10)}`

Where P is the number of eggs laid, x is the number of workers, and y is the daily operating budget (assuming in US dollars $).

A)

We want to find dy/dx.

So, let’s find our equation in terms of x. We can raise both sides to 10/7. Hence:

`\displaystyle P^(10)/(7)=\Big(x^(3)/(10)y^(7)/(10)\Big)^(10)/(7)`

Simplify:

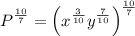
`\displaystyle P^(10)/(7)=x^(3)/(7)y`

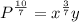
Divide both sides by the x term to acquire:

`\displaystyle y=P^(10)/(7)x^{-(3)/(7)}`

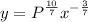
Take the derivative of both sides with respect to x:

`\displaystyle (dy)/(dx)=(d)/(dx)\Big[P^(10)/(7)x^{-(3)/(7)}\Big]`

Apply power rule. Note that P is simply a constant. Hence:

`\displaystyle (dy)/(dx)=P^(10)/(7)(-(3)/(7))(x^{-(10)/(7)})`

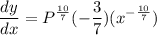
Simplify. Hence, our derivative is:

`\displaystyle (dy)/(dx)=-(3)/(7)P^(10)/(7)x^{-(10)/(7)}`

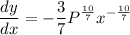
Part B)

We want to evaluate the derivative when x is 30 and when y is $10,000.

First, we will need to find P. Our original equations tells us that:

`P=x^(0.3)y^(0.7)`

Hence, at x = 30 and at y = 10,000, P is:

`P=(30)^(0.3)(10000)^(0.7)`

Therefore, for our derivative, we will have:

`\displaystyle (dy)/(dx)=-(3)/(7)\Big(30^(0.3)(10000^(0.7))\Big)^(10)/(7)\Big(30^{-(10)/(7)}\Big)`

Use a calculator. So:

`\displaystyle (dy)/(dx)=-(1000)/(7)=-142.857142...\approx-143`

Our derivative is given by dy/dx. So, it represents the change in the daily operating cost over the change in the number of workers.

So, when there are 30 workers with a daily operating cost of $10,000 producing a total of about 1750 eggs, the daily operating cost decreases by about $143 per extra worker.