Answer:
The surface area of the cuboid is 378
 square inches.
square inches.
Explanation:
A cuboid is a shape which has six surfaces formed from a rectangle. The surface area of a cuboid is the sum of all its individual ares of each surface.
Given the following dimensions of the cuboid:
length = 10 3/4 in =
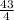 in
in
width = 8 in
height = 5 1/2 in =
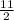 in
in
Since the opposite surface of a cuboid are the same, then;
Area of the 1st surface = length x width
=
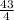 x 8
x 8
= 86 square inches
Area of the 2nd surface = width x height
= 8 x
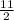
= 44 square inches
Area of the 3rd surface = length x height
=
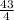 x
x
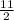
=
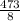
= 59
 square inches
square inches
Surface area of the cuboid = 2 x 86 + 2 x 44 + 2 x
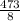
= 172 + 88 + 118.25
= 378.25
Surface area of the cuboid = 378
 square inches
square inches