Question

Can you help me ? Pls

Answer 1

The value of x = 4.4 units.

Explanation:

• Given that figure A is a scale image of Figure B.

It is clear that the two sides are similar, so their corresponding angles will be congruent and corresponding sides are in proportion.

Thus, using the corresponding ratios of figure A and Figure B

`(x)/(4)\:=\:(11)/(10)`

Multiply both sides by 10

`(x)/(4)\cdot \:10=(11)/(10)\cdot \:10`

`(5x)/(2)=11`

`5x=22`

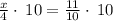
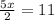
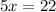
Divide both sides by 5

`(5x)/(5)=(22)/(5)`

`x=(22)/(5)`

`x = 4.4`

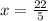
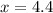
Therefore, the value of x = 4.4 units.