Question

A bus travels at a constant speed. it stops for a short time and then travels at a higher constant speed. draw a distance-time graph for this journey.

Answer 1

See the explanation below

Step-by-step explanation:

Since the bus travels at a constant speed, we can use the following equation.

`x=x_(o)+v*t`

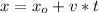
where:

x = final position [m]

xo = initial position = 0 (if the bus starts from some reference point)

v = constant velocity [m/s]

t = time [s]

Let's take some data as an example and then graph them.

v = 2 [m/s]

t = 2 [s]

That is, after two seconds, the final position will be:

`x = 0 + 2*2\\x = 4 [m]`

After the two seconds, the bus stops for about 2 seconds more. Then the bus will go with a velocity of 4 [m/s] for two seconds more.

So the total time is 6 [s].

Let's draw the x-t graph.

• We see that the position changes during the first two seconds, from a position 0 to 4 [m]
• Then the bus stops for two seconds, that is, for 4 seconds the bus has traveled 4 meters.
• Then the bus moves to 4 [m/s], for 2 more seconds. That is, the bus will have moved up to 6 seconds.

And the final offset must be calculated using the same equation.

`x = x_(0)+v*t\\x = 4+4*(6-4)\\x = 4 +8\\x = 12 [m]`