5^(2x-1)+5^(x+1)=250 how do you solve? thank you

Question

asked Nov 26, 2021 206k views

1 Answer

Peter Hawkins · Answer 1 · 2021-11-29T20:25:13+0000

Answer:

x = 2

Explanation:

Exponential Equations

Solve:

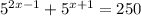
5^(2x-1)+5^(x+1)=250

Separate each exponential:

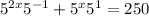
5^(2x)5^(-1)+5^(x)5^(1)=250

Operating:

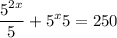
$\displaystyle (5^(2x))/(5)+5^(x)5=250$

Multiplying by 5:

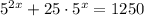
$5^(2x)+25\cdot5^x=1250$

Rearranging:

$5^(2x)+25\cdot5^x-1250=0$

Recall that:

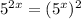
5^(2x)=(5^(x))^2

$(5^(x))^2+25\cdot5^x-1250=0$

Calling

y=5^(x):

y^2+25y-1250=0

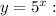
Factoring:

(y-25)(y+50)=0

There are two possible solutions:

y=25

y=-50

Since

y=5^(x)

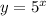
y cannot be negative, thus:

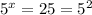
5^(x)=25=5^2

The solution is:

x = 2