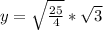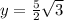Question

Find the missing side lengths. Write your answers in simplest radical form with the denominator rationalized. Please answer the best you can if you choose to answer, as I don't want to give away all my points for nothing.

Answer 1

`x = 5`

`y = (5)/(2)\sqrt3`

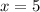
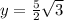
Explanation:

Required

Find x and y

From the triangle, we can see that x is the longest side (i.e. the hypotenuse)

The sin of an angle is:

`\sin(\theta) = (opposite)/(hypotenuse)`

The relationship between the given angle (30 degrees), x and 5/2 is:

`\sin(30) = (5/2)/(x)`

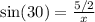
Cross Multiply:

`x * \sin(30) = (5/2)/(x) * x`

`x * \sin(30) = (5)/(2)`

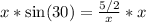
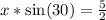
Solve for x

`x = (5)/(2\sin(30))`

`\sin(30) = 0.5`

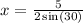
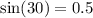
So, the expression becomes

`x = (5)/(2*0.5)`

`x = (5)/(1)`

`x = 5`

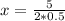
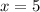
To solve for y, we make use of Pythagoras theorem:

`x^2 = y^2 + (5)/(2)^2`

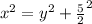
Substitute 5 for x

`5^2 = y^2 + (5)/(2)`

`25 = y^2 + (25)/(4)`

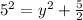
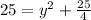
Solve for
`y^2`

`y^2 = 25 - (25)/(4)`

`y^2 = (100 - 25)/(4)`

`y^2 = (75)/(4)`

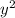
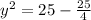
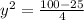
Square root of both sides

`y = \sqrt{(75)/(4)}`

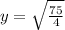
Express 75 as 25 * 3

`y = \sqrt{(25 * 3)/(4)}`

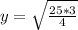
Split:

`y = \sqrt{(25)/(4)} * \sqrt3`

`y = (5)/(2) * \sqrt3`

`y = (5)/(2)\sqrt3`