Question

Please help me please

Answer 1

Please check the explanation.

Explanation:

Given the system of equations

`\begin{bmatrix}x-3y=2\\ 2x+y=11\end{bmatrix}`

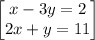
Multiplying the second equation i.e. 2x+y = 11 by 3 and then adding the result to the first equation would eliminate the variable y and the value of x can be determined.

3(2x+y) = 3(11)

6x+3y = 33

Now, adding 6x+3y = 33 to the first equation i.e. x-3y = 2

x - 3y = 2

+

6x + 3y = 33

__________

7x = 35

divide both sides by 7

7x/7 = 35/7

x = 5

so, the value of x = 5.

Therefore, we conclude that in order to solve the system of equations using elimination methods, we can multiply the second equation i.e. 2x+y = 11 by 3, and then adding the result to the first equation would eliminate the variable y and the value of x can be determined.

Hence, option (a) is true.

BONUS: SOLVING THE REMAINING PORTION to determine y

As

x = 5

substituing x = 5 in x - 3y = 2

x - 3y = 2

5 - 3y = 2

5 - 2 = 3y

3 = 3y

y = 1

Therefore,

x = 5

y = 1