Answer:
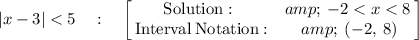
The graph is also attached.
Explanation:
Given the expression
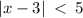
Apply absolute rule:
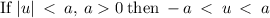
so the expression becomes
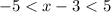
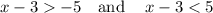
solving condition 1
x−3<5
Add 3 to both sides
x−3+3<5+3
x<8
solving condition 2
x−3>−5
Add 3 to both sides
x−3+3>−5+3
x>−2
combining the intervals
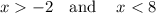
Merging overlapping intervals
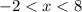
Therefore,
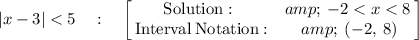
The graph is also attached.