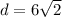Answer:
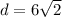
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Algebra II
- Distance Formula:
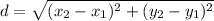
Explanation:
Step 1: Define
Point R (-4, 1)
Point S (2, 7)
Step 2: Find distance d
Simply plug in the 2 coordinates into the distance formula to find distance d
- Substitute [DF]:
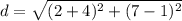
- Add/Subtract:
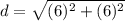
- Exponents:
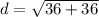
- Add:
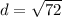
- Simplify: