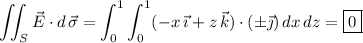The flux of
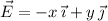 is given by the surface integral
is given by the surface integral
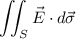
where
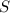 is the given square region, which we can parameterize by
is the given square region, which we can parameterize by
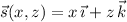
with
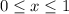 and
and
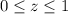 . The area element is
. The area element is
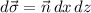
where
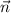 is the normal vector to
is the normal vector to
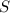 . Depending on the orientation of
. Depending on the orientation of
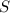 , this vector could be
, this vector could be
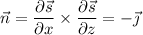
or
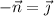 ; either way, the integral reduces to
; either way, the integral reduces to