Given :
The half life of uranium 232 is 70 years.
To Find :
How many half lives will it take for 10 grams of it to be reduced to 1.25 grams.
Solution :
We know, formula of radioactive decay is :
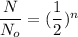
Here,
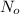 is initial amount and N is remaining amount.
is initial amount and N is remaining amount.
Putting all given values in above equation, we get :
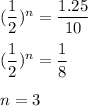
Therefore, it takes 3 half lives i.e. 210 years to reduced to 1.25 grams.