Question

Write the equation of the line that passes through the given point and is parallel to the given line.

Keep all fractions in improper form

Answer 1

(Note: this answer is assuming that the equation has to be put in slope-intercept format.)

Answer:

`y = (1)/(2) x - (5)/(2)`

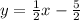
Explanation:

1) Let's use the point-slope formula to determine what the answer would be. To do that though, we would need two things: the slope and a point that the equation would cross through. We already have the point it would cross through, (-3,-4), based on the given information. So, in the next step, let's find the slope.

2) We know that the slope has to be parallel to the given line,
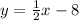`y = (1)/(2)x - 8`. Remember that slopes that are parallel have the same slope - so, let's simply take the slope from the given equation. Since it's already in slope-intercept form, we know that the slope then must be
`(1)/(2)`.

3) Finally, let's put the slope we found and the x and y values from (-3, -4) into the point-slope formula and solve:

`(y- (-4)) = (1)/(2) (x - (-3))\\y + 4 = (1)/(2) (x + 3))\\y + 4 = (1)/(2)x+ (3)/(2) \\y = (1)/(2)x + (3)/(2) - 4\\y = (1)/(2)x + (3)/(2) - (8)/(2) \\y = (1)/(2)x - (5)/(2)`

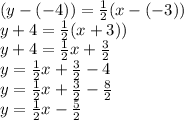
Therefore,
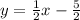`y = (1)/(2)x - (5)/(2)` is our answer. If you have any questions, please do not hesitate to ask!