Question

Derive the equation of the parabola with a focus at (−5, 5) and a directrix of y = −1​

Answer 1

Explanation:

If you plot the focus and the directrix you see that the focus is above the directrix. Since a parabola always wraps itself around the focus, this parabola opens upwards and has the standard form equation:

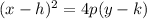`(x-h)^2=4p(y-k)` where h and k are the coordinates of the vertex and p is the number of units between the vertex and the focus, or the vertex and the directrix. This number of units will be the same for both since the vertex is smack dab inbetween the focus and the directrix. The focus is also on the axis of symmetry, which means that it shares the x coordinate with the vertex (which is actually the h coordinate) of -5. Halfway between the y value of 5 and the y value of -1 is 2. So the vertex is located at (-5, 2). The number of units between the vertex and the focus is 3, so the equation is:

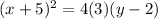`(x+5)^2=4(3)(y-2)` and simplify a bit to

`(x+5)^2=12(y-2)`

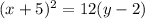
I'm not sure how far down you need to simplify that. Taking it a few steps further gives you:

`(1)/(12)(x+5)^2=y-2` and then to

`(1)/(12)(x+5)^2+2=y`

It all depends upon the form you're being asked for.