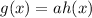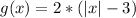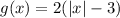Question

If f\left(x\right)=\mid x\midf ( x ) =∣ x ∣, then what is the new function g\left(x\right)g ( x ) when f\left(x\right)f ( x ) is translated 3 units down, followed by a vertical stretch of 2? Group of answer choices

Answer 1

`g(x) = 2 (|x| - 3)`

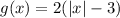
Explanation:

Given

`f\left(x\right)=\mid x\mid`

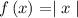
Translation = 3 units down

Vertical stretch of 2 to give g(x)

Required

`g\left(x\right)`

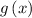
3 units down translation

A function is translated down as follows:

`h(x) = f(x) - k`

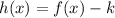
Where k is the number of units.

So:

`h(x) = f(x) - k`

`h(x) = |x| - 3`

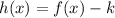
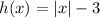
Vertical stretch of 2

A function is vertically stretched as follows;

`g(x) = ah(x)`

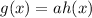
Where a is the units stretched.

In this case:

`a = 2`

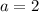
So:

`g(x) = ah(x)`

`g(x) = 2 * (|x| - 3)`

`g(x) = 2 (|x| - 3)`