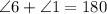Question

Lines x and y are parallel and are cut by the transversal b. If the measure of angle 1 is 57°, what is the measure of angle 6? Explain the relationship between the two angles.

Answer 1

`\angle6=123`

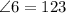
Explanation:

Given

Lines x and y

Transversal b

`\angle 1 = 57`

Required

Find
`\angle 6`

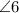
From the attachment,
`\angle1` and
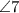`\angle7` are vertically opposite.

This means that

`\angle 1 =\angle 7 = 57`

Similarly

`\angle 7` and
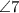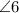`\angle 6` are supplementary angles

So:

`\angle7 + \angle6=180`

Make
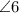`\angle6` the subject

`\angle6=180-\angle7`

`\angle6=180-57`

`\angle6=123`

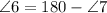
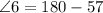
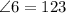
The relationship between
`\angle1` and
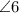`\angle6` is that they are supplementary angles because:

`\angle6+ \angle1=180`